Drawing A Slope Field
Drawing A Slope Field - For dy dx x2 −2, this would be slope field x2 −2. Clearly, t t t is the independent variable, and y y y is a function of t. Therefore by drawing a curve through consecutive slope lines, you can find a solution to the differential equation. Therefore by drawing a curve through consecutive slope lines, you can find a solution to the differential equation. We'll learn in a few sections how to solve this kind of equation, but for now we can't get an explicit solution. Forming a slope field slope fields & equations slope fields & equations google classroom which differential equation generates the slope field? We'll illustrate this with a simple example: This shows us the rate of change at every point and we can also determine the curve that is formed at every single point. Equation from slope field worked example: Web in this video, i will show you how to draw a slope field, also known as the direction field, which can be drawn from a differential equation y' = f(x,y). Web given a differential equation in x and y, we can draw a segment with dy/dx as slope at any point (x,y). Clearly, t t t is the independent variable, and y y y is a function of t. Web the slope field is a cartesian grid where you draw lines in various directions to represent the slopes of the. That's the slope field of the equation. At a point \((x,y)\), we plot a short line with the slope \(f. We'll illustrate this with a simple example: Discover any solutions of the form y= constant. For instance, suppose you had the differential equation: Web explore math with our beautiful, free online graphing calculator. Match a slope field to a differential equation. Web 5 years ago observe that you can draw infinitely many possible graphs for a given slope field. Web brian mclogan 1.29m subscribers 3.7k views 5 years ago differential equations learn how to create slope fields and sketch the particular solution to. Web given a differential equation in x and y, we can draw a segment with dy/dx as slope at any point (x,y). And this is the slope a solution \(y(x)\) would have at \(x\) if its value was \(y\). D y d x = x + y a Web drawing paths in the plane that are parallel to the nearby. Web the slope field is a cartesian grid where you draw lines in various directions to represent the slopes of the tangents to the solution. The slope field is utilized when you want to see the tendencies of solutions to a de, given that the solutions pass through a certain localized area or set of points. Match a slope field. Web the slope field is a cartesian grid where you draw lines in various directions to represent the slopes of the tangents to the solution. That's the slope field of the equation. In other words, \(f(x,y)\) is the slope of a solution whose graph runs through the point \((x,y)\). D y d x = x + y a Web given. The slope field is utilized when you want to see the tendencies of solutions to a de, given that the solutions pass through a certain localized area or set of points. Web brian mclogan 1.29m subscribers 3.7k views 5 years ago differential equations learn how to create slope fields and sketch the particular solution to a differential equation. Web drawing. Web slope fields allow us to analyze differential equations graphically. Web a slope field is a visual representation of a differential equation in two dimensions. And this is the slope a solution \(y(x)\) would have at \(x\) if its value was \(y\). Web draws the slope (direction) field for the given differential equation y' = f(x,y).the movable black point sets. A slope field doesn't define a single function, rather it describes a class of functions which are all solutions to a particular differential equation. Web brian mclogan 1.29m subscribers 3.7k views 5 years ago differential equations learn how to create slope fields and sketch the particular solution to a differential equation. Learn how to draw them and use them to. Web 5 years ago observe that you can draw infinitely many possible graphs for a given slope field. A direction field (or slope field / vector field) is a picture of the general solution to a first order differential equation with the form. Web given a differential equation in x and y, we can draw a segment with dy/dx as. Web slope fields allow us to analyze differential equations graphically. Match a slope field to a differential equation. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Using a visualization of a slope field, it is easy to. Slope field from equation worked example: In other words, \(f(x,y)\) is the slope of a solution whose graph runs through the point \((x,y)\). That's the slope field of the equation. Web given a differential equation in x and y, we can draw a segment with dy/dx as slope at any point (x,y). Match a slope field to a solution of a differential equation. And this is the slope a solution \(y(x)\) would have at \(x\) if its value was \(y\). Web draws the slope (direction) field for the given differential equation y' = f(x,y).the movable black point sets the initial condition of an approximated particular solution drawn with euler's method. Sketching slope fields slope fields introduction worked example: The slope field is utilized when you want to see the tendencies of solutions to a de, given that the solutions pass through a certain localized area or set of points. Discover any solutions of the form y= constant. Therefore by drawing a curve through consecutive slope lines, you can find a solution to the differential equation. So each individual point of a slope field (or vector field) tells us the slope of a function.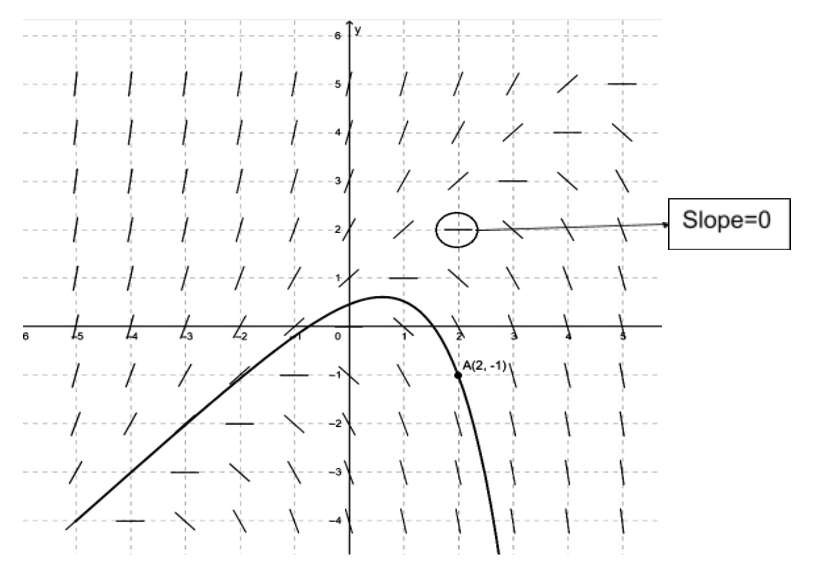
How do you draw the slope field of the differential equation \\[{{y

Worked example slope field from equation AP Calculus AB Khan
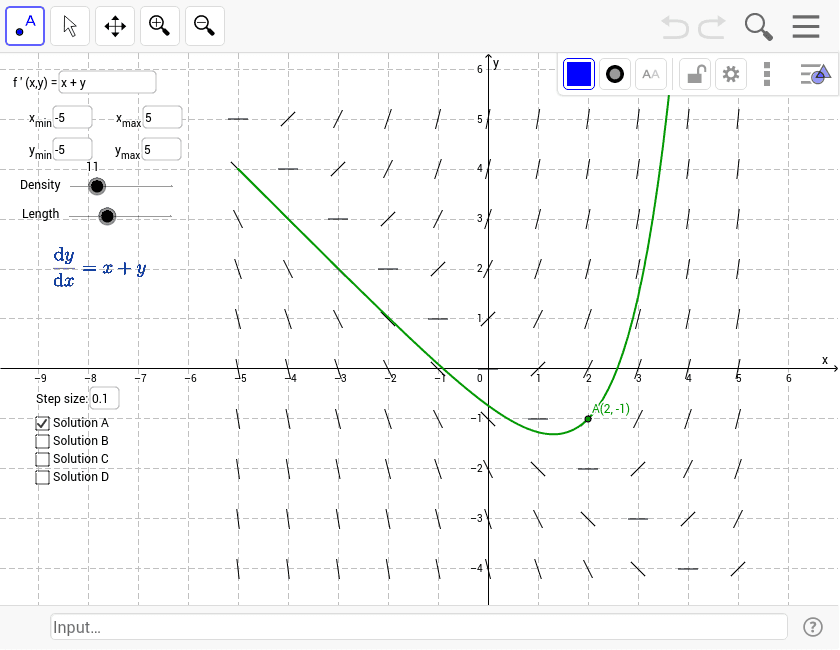
Slope field plotter GeoGebra

Slope Fields_Example 2 on how to sketch a slope field YouTube

Calculus AB/BC 7.3 Sketching Slope Fields YouTube

Sketch the slope field and sketch the particular equation YouTube
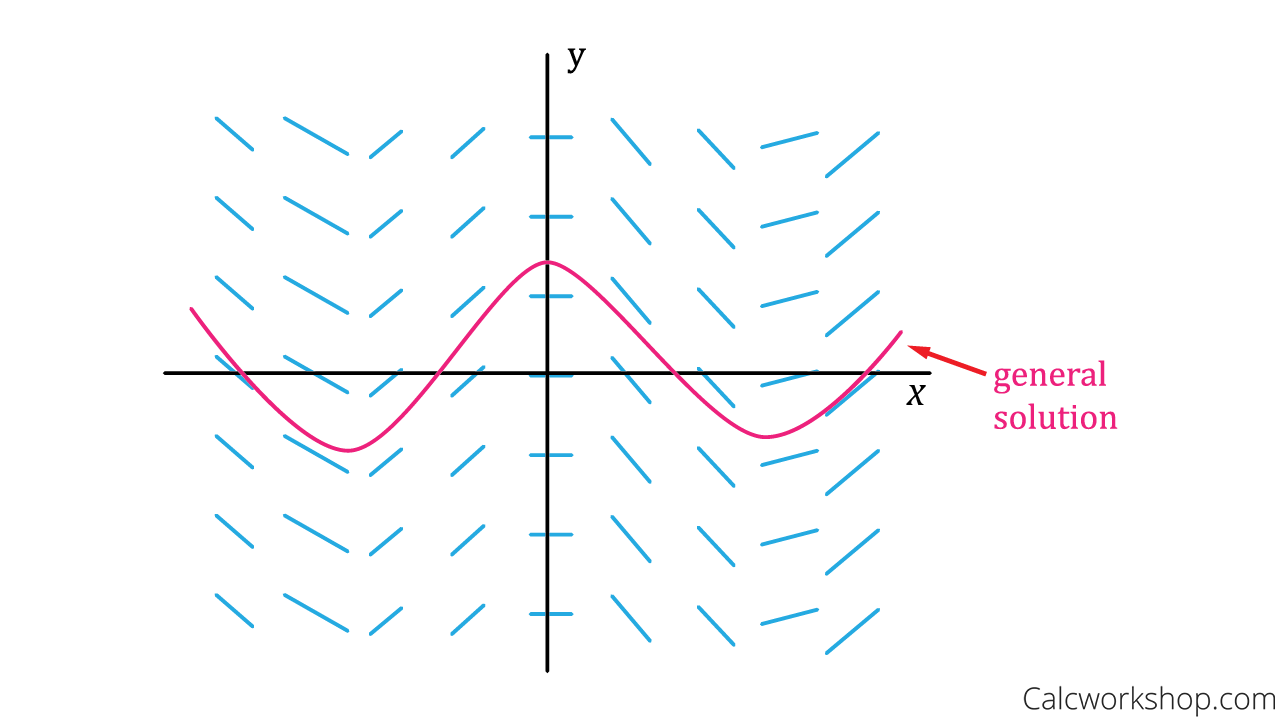
Slope Fields

PPT Slope Field & Particular Solutions PowerPoint Presentation ID
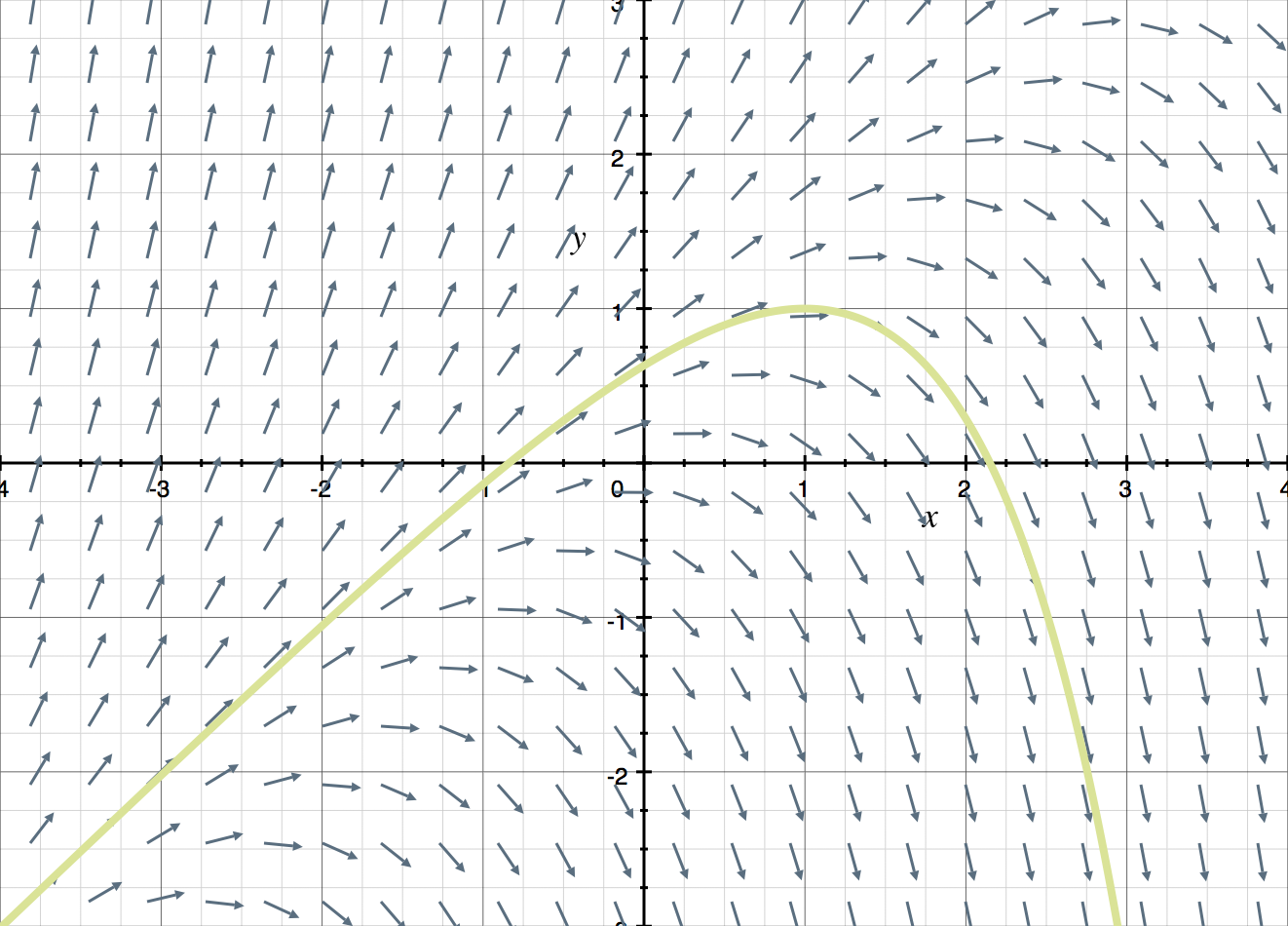
How to sketch direction fields — Krista King Math Online math help
Slope Fields Calculus YouTube
See How We Determine The Slopes Of A Few Segments In The Slope Field Of An Equation.
For Dy Dx X2 −2, This Would Be Slope Field X2 −2.
We'll Learn In A Few Sections How To Solve This Kind Of Equation, But For Now We Can't Get An Explicit Solution.
For Instance, Suppose You Had The Differential Equation:
Related Post: