First Derivative Sign Chart
First Derivative Sign Chart - Web 4.5.1 explain how the sign of the first derivative affects the shape of a function’s graph. Web you can use sign charts to analyze the behavior of a function. Web explain how the sign of the first derivative affects the shape of a function’s graph. Graph of derivative to original function. 4.5.3 use concavity and inflection points to explain how the sign of the second derivative affects the shape of. Get a grid of sign charts for a function and its first and second derivatives. See the adjoining sign chart for the first derivative, f '. The first derivative sign chart for a function f whose derivative is given by the formula f' (x) = e −2x (3 − x)(x + 1) 2. Web explain how the sign of the first derivative affects the shape of a function’s graph. Web a sign diagram of the first derivative, f'(𝑥) can be made. Web here are instruction for establishing sign charts (number line) for the first and second derivatives. Web how does the first derivative of a function reveal important information about the behavior of the function? Consider the graph of the function. Web explain how the sign of the first derivative affects the shape of a function’s graph. How do you find. Explain the concavity test for a function over an open interval. Web the top graph is the original function, f (x), and the bottom graph is the derivative, f’ (x). Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. Web here are instruction for establishing sign charts (number. 4.5.2 state the first derivative test for critical points. For x =0 and x =2. Here, it’s important to keep your head in the game. They help you find maxima, minima and saddle points. Web here are instruction for establishing sign charts (number line) for the first and second derivatives. Web a sign diagram of the first derivative, f'(𝑥) can be made. In the regions between these points, a positive sign is written when the function is increasing and a negative sign is written when the function is decreasing. This is how you do it: What information can we determine about the function using the first derivative? In a sign. Now determine a sign chart for the second derivative, f '' : Web the top graph is the original function, f (x), and the bottom graph is the derivative, f’ (x). In this question, we are given the curve of 𝑦 = 𝑓 ′ ( 𝑥) and asked to find the intervals on which 𝑓 ( 𝑥) is increasing. Drawing. Web a sign diagram of the first derivative, f'(𝑥) can be made. Web this can be done in many ways, but we like using a sign chart. State the first derivative test for critical points. The first derivative sign chart for a function f whose derivative is given by the formula f' (x) = e −2x (3 − x)(x +. Web 493k views 6 years ago new calculus video playlist. Explain the concavity test for a function over an open interval. Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. This is how you do it: Web derivativesigncharts | wolfram function repository. Web f' is the derivative of f, and f'' is the second derivative of f, which is the first derivative of f'. Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. State the first derivative test for critical points. What do you notice about each pair? Web explain. Web this can be done in many ways, but we like using a sign chart. Web f' is the derivative of f, and f'' is the second derivative of f, which is the first derivative of f'. What information can we determine about the function using the first derivative? How do you find the interval in which the function f. Now determine a sign chart for the first derivative, f ' : Web what information does the first derivative tell you? Every order of derivative after is just the derivative of the function before that. Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. Web what follows is. Use concavity and inflection points to explain how the sign of the second derivative affects the shape of a function’s graph. On what intervals is 𝑓 increasing or decreasing? How can we use the first derivative test. For x =0 and x =2. Graph of derivative to original function. Web the top graph is the original function, f (x), and the bottom graph is the derivative, f’ (x). The first derivative test can be used to locate. Here, it’s important to keep your head in the game. Web we create a first derivative sign chart to summarize the sign of f' on the relevant intervals along with the corresponding behavior of f. This is how you do it: Web here are instruction for establishing sign charts (number line) for the first and second derivatives. How do you find values of t in which the speed of the particle is increasing if he position of a particle moving along a line is given by s(t) = 2t3 − 24t2 + 90t + 7 for t ≥ 0? 4.5.2 state the first derivative test for critical points. Consider the graph of the function. Web how does the first derivative of a function reveal important information about the behavior of the function? State the first derivative test for critical points.
Making and Interpreting Sign Charts (First and Second Derivatives

Chart Of Derivatives
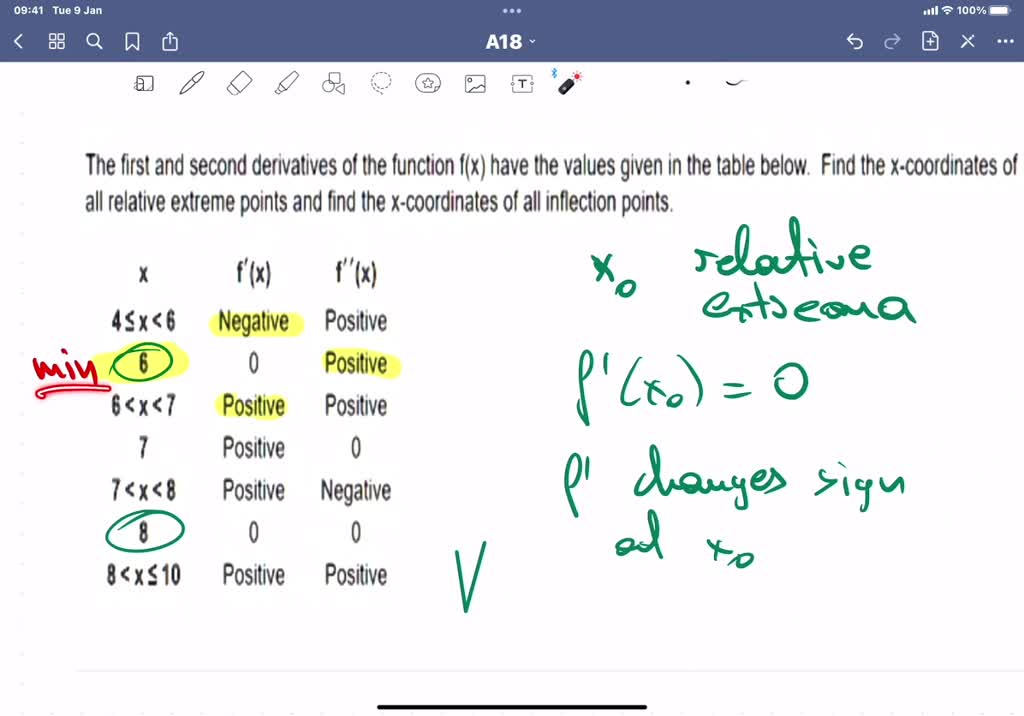
SOLVED Below you see the first derivative sign chart (the sign chart

Derivative Rules Cheat Sheet Calculus Ace Tutors Blog
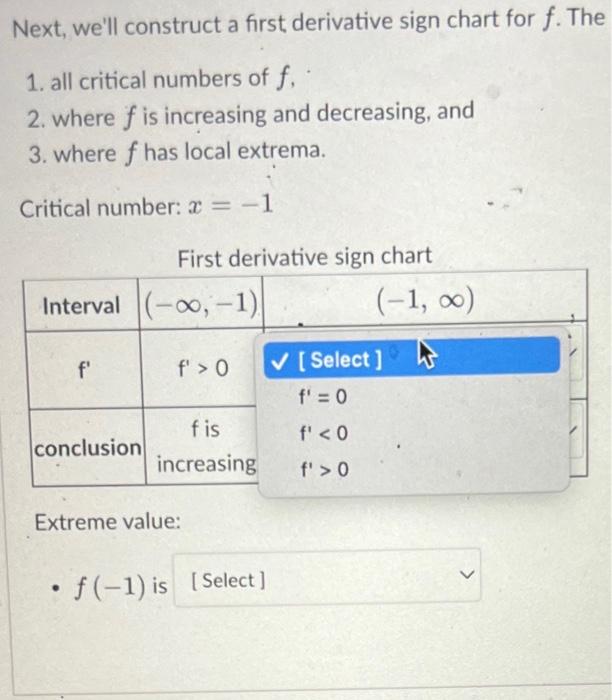
next well construct a first derivative sign chart for f the 1 all

First Derivative Test eMathHelp

3.3 First Derivative Test / Slope Shuford's Site
![[Math] How to identify the graph of a function and the graphs of its](https://i.stack.imgur.com/vze2T.png)
[Math] How to identify the graph of a function and the graphs of its
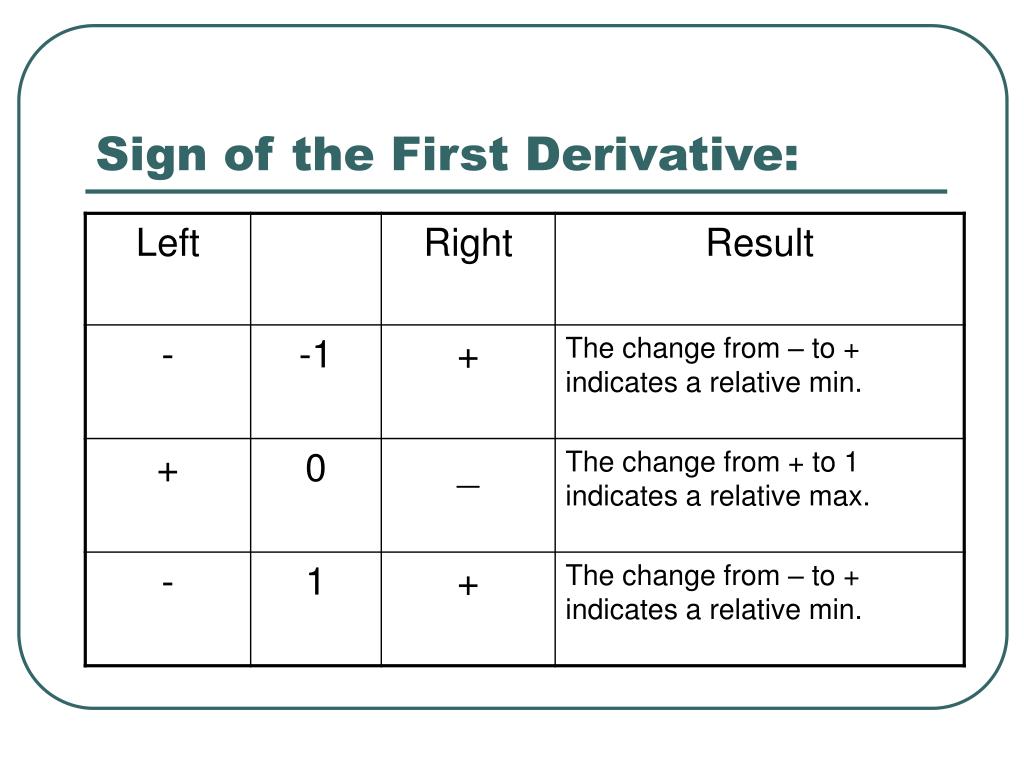
PPT Applications of Derivatives PowerPoint Presentation, free

How to Understand Sign Diagrams
What Information Can We Determine About The Function Using The First Derivative?
Now Determine A Sign Chart For The Second Derivative, F '' :
4.5.3 Use Concavity And Inflection Points To Explain How The Sign Of The Second Derivative Affects The Shape Of.
This Calculus Video Tutorial Provides A Basic Introduction Into The First Derivative Test.
Related Post: