How To Draw A Bifurcation Diagram
How To Draw A Bifurcation Diagram - Web a phase line diagram for the autonomous equation y0 = f(y) is a line segment with labels sink, source or node, one mark and label for each root y of f(y) = 0, i.e., each equilibrium; Web please see the below answers on the same lines which discuss the steps to plot the bifurcation diagrams:. Finally, the matrix sign function, nonlinear equation and. Web a phase line diagram for the autonomous equation y′ = f(y) is a line segment with labels sink, source or node, one for each root of f(y) = 0, i.e., each equilibrium; Web we go over basic definitions and use phase and bifurcation diagrams to describe the dynamics of first order autonomous differential equations. Web the bifurcation diagram is shown in fig. Array_like these values are appended to a copy of arr.it must be of the correct shape (the same shape as arr, excluding axis). If axis is not specified, values can be any. Web this time, jeff explains how to create bifurcation diagrams that plot the number and types of fixed points against the value of a parameter for a family of discrete dynamical systems. However, as the code is quite complicated i am not sure how to edit the code so that it deals with. Web we go over basic definitions and use phase and bifurcation diagrams to describe the dynamics of first order autonomous differential equations. The ratio of the lengths of successive intervals between values of r for which bifurcation occurs converges to the first feigenbaum constant. I'm considering the ordinary differential equation (ode) du/dt = a +u2 −u5 d u / d. Bifurcation diagram for y = y(y − 3)2 + k. Web the bifurcation diagram is shown in fig. However, as the code is quite complicated i am not sure how to edit the code so that it deals with. Web download full book (pdf) resources expand_more. We can imagine what happens to \(x\) as \(r\) increases from negative values, supposing. Web we go over basic definitions and use phase and bifurcation diagrams to describe the dynamics of first order autonomous differential equations. Web upon solving the cube equation y(y − 3)2 + k = 0, we obtain the real critical point. However, as the code is quite complicated i am not sure how to edit the code so that it. Web to create a bifurcation diagram for a given differential equation containing a single parameter a: It summarizes the contents of a direction field and threaded curves, including all equilibrium solutions. Differential equations, 4th edition (by blanchard, devaney, and hall): Web differential equations and linear algebra lecture 10a. Web learn how to graph a bifurcation diagram for an autonomous differential. Web this time, jeff explains how to create bifurcation diagrams that plot the number and types of fixed points against the value of a parameter for a family of discrete dynamical systems. Finally, the matrix sign function, nonlinear equation and. The blue represent stable and red unstable, that is unstable region is when $\lambda = [0, +\infty)$. Web the bifurcation. Web learn how to graph a bifurcation diagram for an autonomous differential equation with a parameter that directly affects the solution end behavior about one o. Web here is an example of how to draw a bifurcation diagram in python: For a dynamical system , bifurcation points are those equilibrium points at which the jacobian is singular. Web this time,. Web a bifurcation diagram summarises all possible behaviours of the system as a parameter is varied. It summarizes the contents of a direction field and threaded curves, including all equilibrium solutions. We can think of these as discrete points in time and each point represents a fixed $\lambda$. Web upon solving the cube equation y(y − 3)2 + k =. This demonstration shows the bifurcation diagrams of several normal form bifurcations in one dimension. For a dynamical system , bifurcation points are those equilibrium points at which the jacobian is singular. Web a phase line diagram for the autonomous equation y′ = f(y) is a line segment with labels sink, source or node, one for each root of f(y) =. Web this time, jeff explains how to create bifurcation diagrams that plot the number and types of fixed points against the value of a parameter for a family of discrete dynamical systems. It represents all fixed points of the system and their stability as a function of the varying parameter. If axis is not specified, values can be any. Y. Differential equations, 4th edition (by blanchard, devaney, and hall): Array_like values are appended to a copy of this array. I'm considering the ordinary differential equation (ode) du/dt = a +u2 −u5 d u / d t = a + u 2 − u 5. Web this time, jeff explains how to create bifurcation diagrams that plot the number and types. Explore the graph of dy dt = f(y) d y d t = f ( y) to locate. Web we go over basic definitions and use phase and bifurcation diagrams to describe the dynamics of first order autonomous differential equations. I know that the number of fixed points varies based on the value of a a, and i've identified the intervals of a a which correspond with the existence of 1, 2, 1, 2, or 3 3 fixed points. Web upon solving the cube equation y(y − 3)2 + k = 0, we obtain the real critical point. Web however, there is still a way to visualize bifurcation diagrams numerically by simulating the behavior of the system explicitly and then collecting the actual states the system visits for a certain period of time. Web this time, jeff explains how to create bifurcation diagrams that plot the number and types of fixed points against the value of a parameter for a family of discrete dynamical systems. We can think of these as discrete points in time and each point represents a fixed $\lambda$. You may find it helpful to do the following as you begin: Web sketch a bifurcation diagram with respect to the parameter $\alpha$. This demonstration shows the bifurcation diagrams of several normal form bifurcations in one dimension. It summarizes the contents of a direction field and threaded curves, including all equilibrium solutions. Finally, the matrix sign function, nonlinear equation and. The bifurcation diagram for this example is drawn in figure 8.3. Web the bifurcation diagram shows the influence of parameter selection on the iteration sequence. Then we can plot their distributions in a diagram. Web examples and explanations for a course in ordinary differential equations.ode playlist: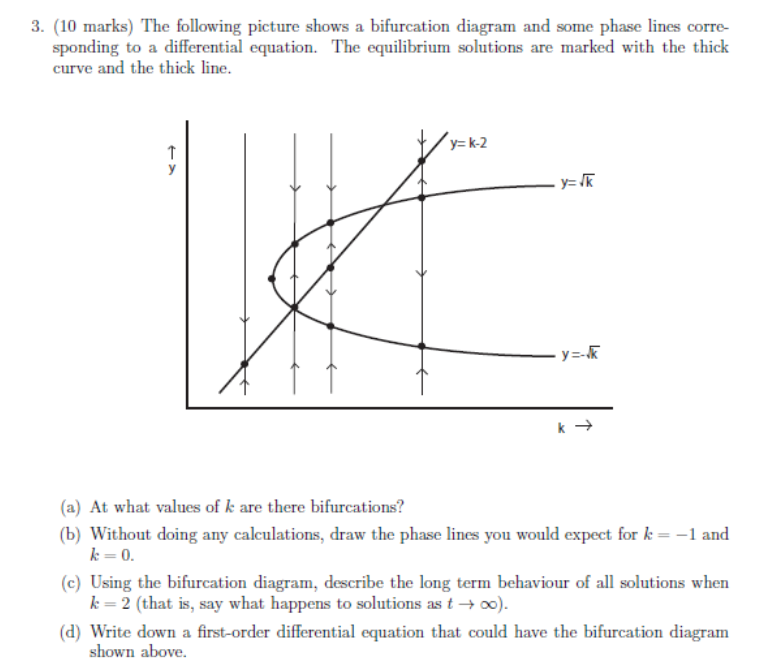
How To Draw Bifurcation Diagram Wiring Diagram Database

GitHub mackondy/bifurcationdiagram MatLab Script for the

2D bifurcation diagrams. (A) Bifurcation diagram obtained as a function

maxresdefault.jpg
How to draw bifurcation Diagram for SIR model using matlab or maple

How to interpret the bifurcation diagram? ResearchGate

Bifurcation Diagram MathBio

How To Draw Bifurcation Diagram General Wiring Diagram
How To Draw Bifurcation Diagram Free Diagram For Student
What is Bifurcation Theory? Wave phenomena
Draw Curves To Show The Location Of The Equilibria As A Function $\Alpha$.
We Can Imagine What Happens To \(X\) As \(R\) Increases From Negative Values, Supposing There Is Some Small Noise In The System So That \(X = X(T)\) Will Diverge From.
Differential Equations, 4Th Edition (By Blanchard, Devaney, And Hall):
A Phase Line Diagram Summarizes The Contents Of A Direction Eld And All Equilibrium Solutions.
Related Post:
